In the second part of this four part series, I will look at how well hitter walk rate can be modeled by plate discipline. I highly recommend reading the first installment, as much of the methodology is the same. Due to this similarity, I will omit most of the methodology in this piece.

Methodology

I am working with the same data set and with the same features as last time. However, there are still several new points I want to mention.

Before looking into the data, my intuition was that O-Swing would be the most influential feature. Out of all the features, O-Swing has the most obvious relationship to walk rate; swinging at a pitch outside of the strike zone will almost never be beneficial in taking a walk. Fouling off a borderline pitch in a two-strike count is a possible exception to this, but even in this situation a hitter seeking a walk is probably better off taking the pitch. I also thought Z-Swing would have a moderately negative effect on walk rate, as swinging at more pitches in the zone likely means shorter plate appearances (PAs) and fewer walks. I did not expect the two contact statistics to be very helpful but thought they could low contact rates could possibly be linked to higher walk rates because more contact usually means shorter PAs. Zone and F-Strike are fairly simple, as high values in either mean less balls and thus fewer walks.

Looking at the marginal correlations between each statistic and walk rate, the results aligned up pretty well with my intuition. O-Swing had the highest correlation easily with -0.708, followed by F-Strike at -0.575. All of the other correlations were also negative and around -0.20. I did not expect F-Strike’s relationship to walk rate to be the second highest after O-Swing, which means I once again underestimated F-Strike’s importance. I also expected Z-Swing’s correlation to be higher.

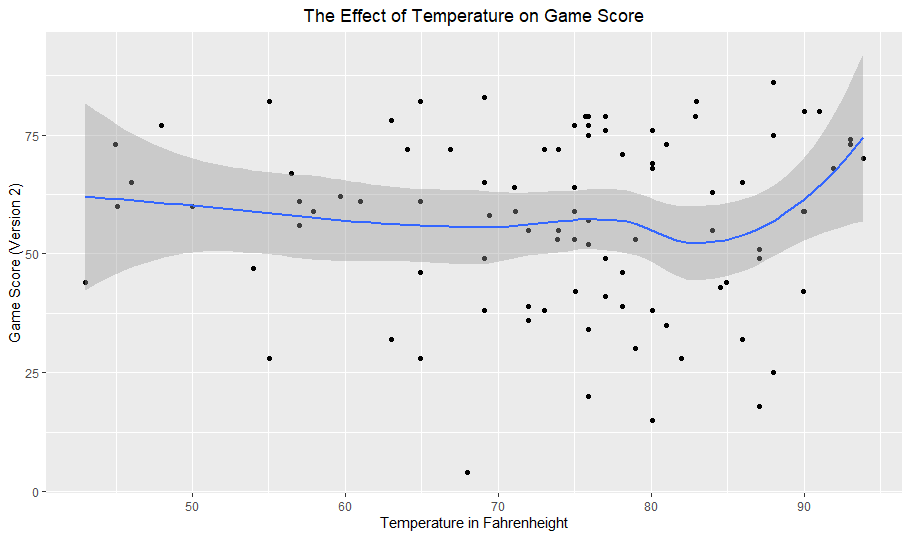
The individual O-Swing and F-Strike versus walk rate plots reveal some interesting findings:

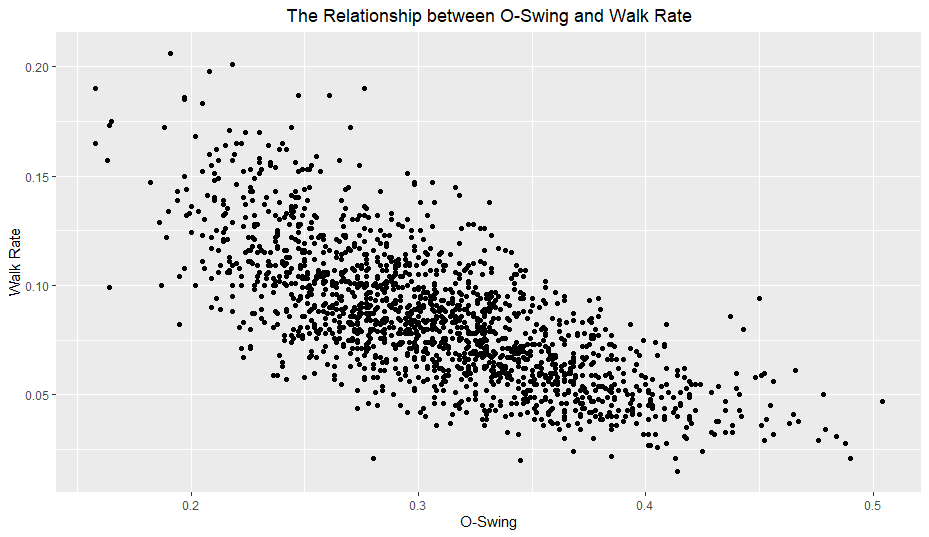
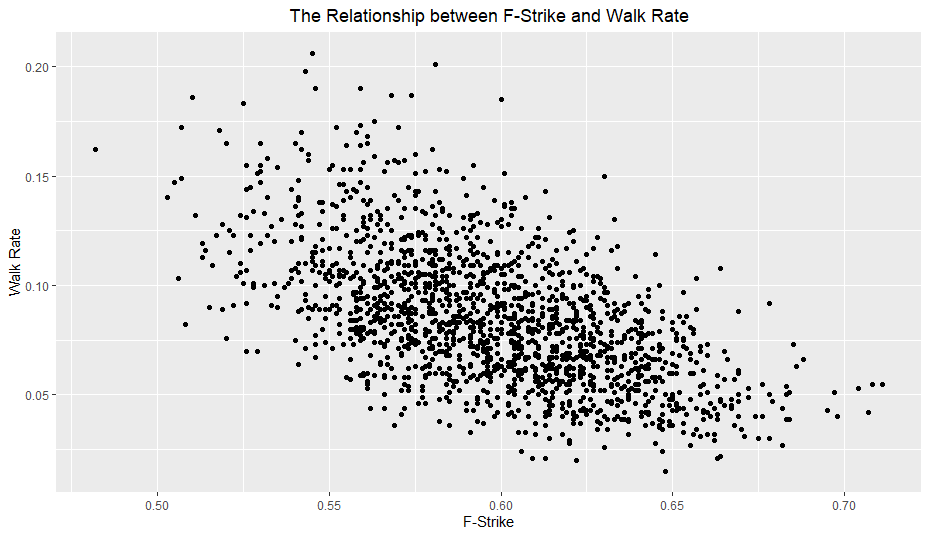
Both O-Swing and F-Strike appear to have a somewhat non-linear relationship with walk rate. I planned on looking at polynomial terms for all variables anyway, but I will especially keep an eye on these two variables.

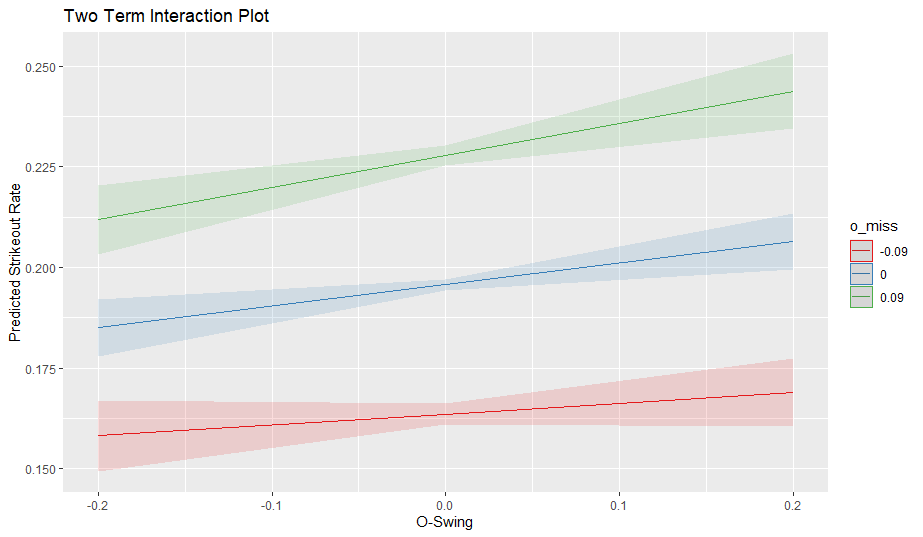
I will test all of the same interaction terms as last time with one difference; I will use O-Contact instead of O-Miss. For strikeout rate, O-Swing and O-Miss work in the same direction (high values of both together should lead to high strikeout rates) but for walk rate, high values of O-Swing and O-Contact together should lead to lower walk rates (high swings at balls + high contact = lower walk rate). Thus, I will simply replace O-Miss for O-Contact for this article.

For this analysis, my regression methods of choice were standard multiple linear regression, ridge regression, and several regression tree techniques including bagging, random forests, and boosting. I decided against using lasso because I am already testing which variables meaningfully improve standard multiple regression (in terms of cross validation mean squared error), so using lasso would be somewhat redundant.

Results

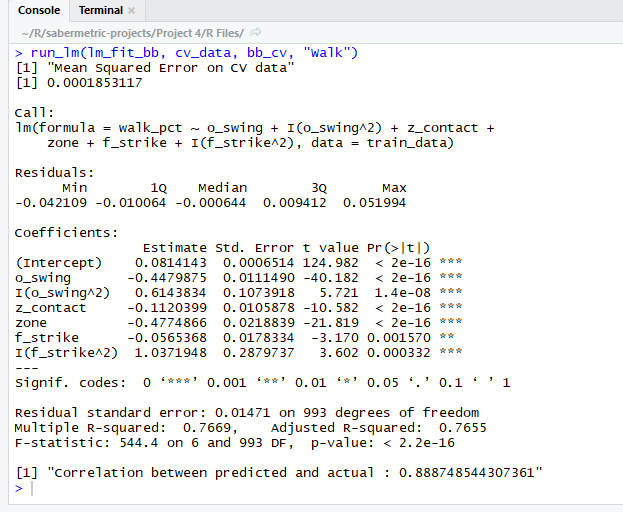
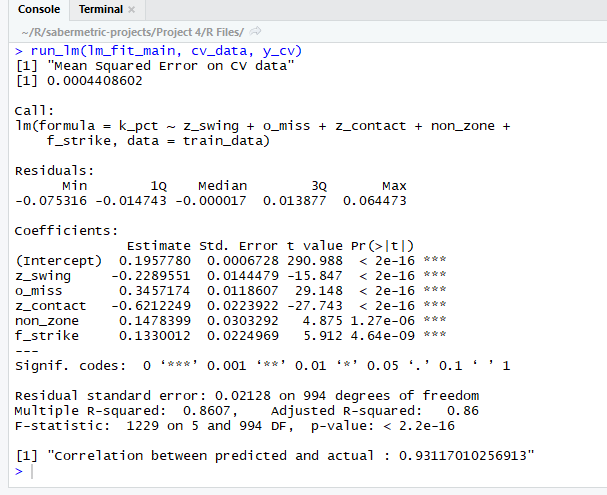
There were several tough decisions I made when selecting my final model. While the O-Swing ^ 2 term is significant (p-value of 1.4e-8 in the above output), it only slightly reduced the CV MSE (cross validation mean squared error). Even though the drop in error was slight (about one percent), it was enough for me to include it in the final model due to very small p-value and graphical evidence. However, I can definitely understand omitting it for model interpretability’s sake. On the other hand, the F-Strike ^ 2 was not nearly as significant in terms of p-value, yet it caused a sizable drop to the CV MSE, making it an easy choice to include. I also ran an ANOVA test comparing this model to the same model without the polynomial terms and found a very small p-value (less than 1e-9), providing more evidence for the polynomial terms.

Another choice I made was omitting the O-Swing * O-Contact and Z-Swing * Z-Contact interaction terms, despite the fact that they had significant p-values. I chose to do this because one, the p-values were not extremely low (around 0.01) and two, neither term helped the CV MSE meaningfully.

Somewhat surprisingly, both Z-Swing and O-Contact did not individually add anything to the regression and in fact increased the CV MSE when added. This was another reason I omitted the interaction terms; typically, when you include interaction terms, you also include the main effects. In this case, including the main effects actually hurt the model’s performance on the CV set.

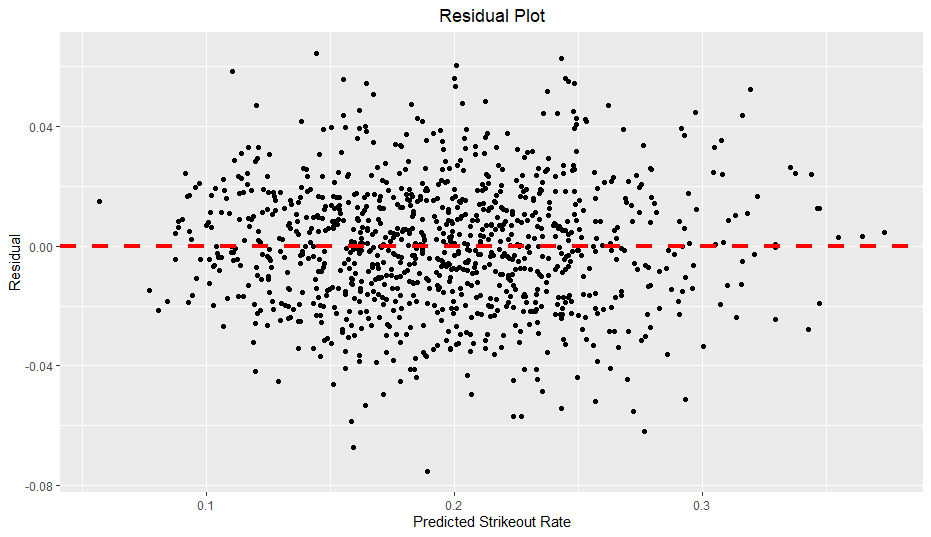
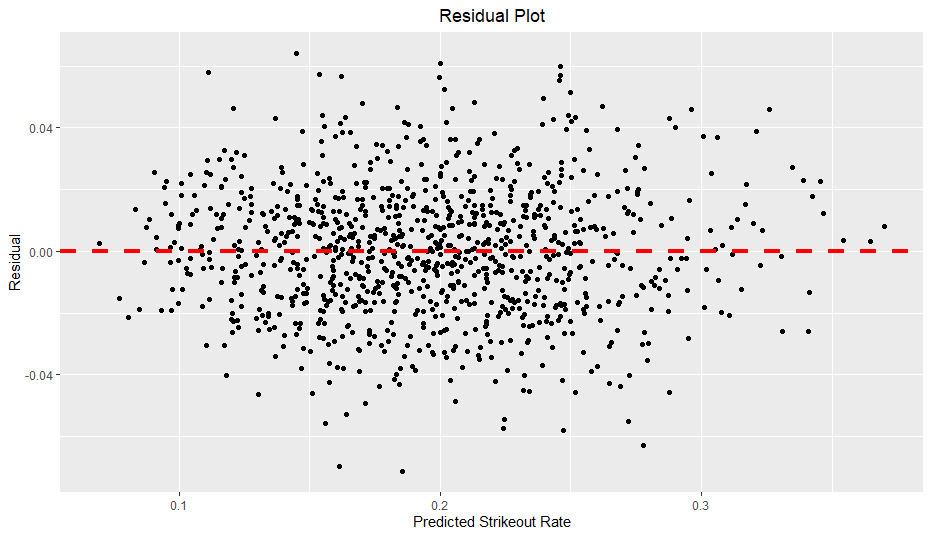
One problem with this model, however, is heteroscedasticity.

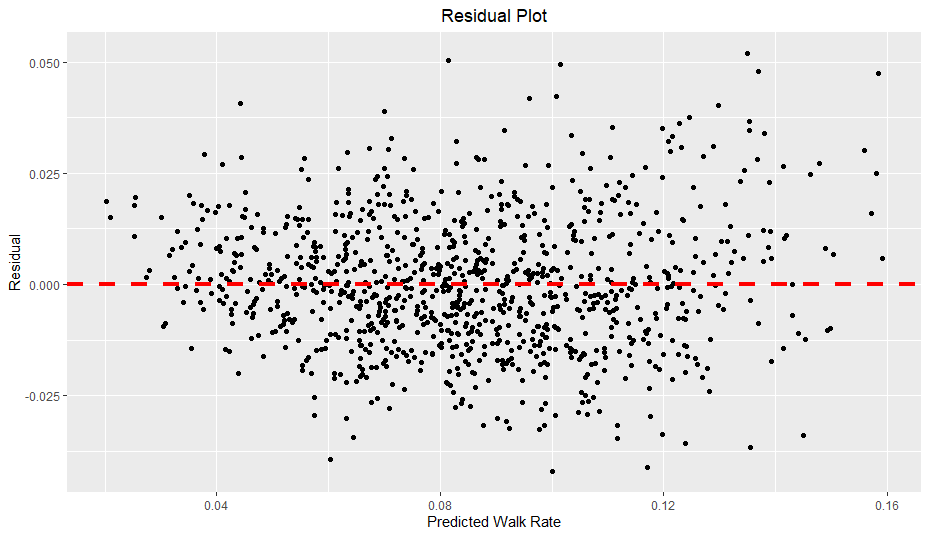
As you can see, as predicted walk rate increases, the residual range seems to expand slightly, creating a slight funnel shape. Of particular note, when the predicted walk rate is over 0.12, the residuals seem to increase in magnitude, especially in regards to positive residuals. In other words, the model seems to underestimate walk rates when the prediction is above 0.12 and generalizes poorly on more extreme walk rates. I also verified the presence of heteroscedasticity with the Breusch-Pagan test, which also found strong evidence of heteroscedasticity. When there is heteroscedasticity in linear regression, the standard errors can be significantly off, so I also found robust standard errors using the sandwich and lmtest packages (similar to here).

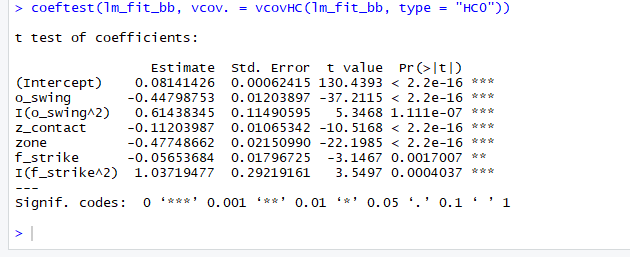
Fortunately in this case, all of the terms are still significant and the standard errors were not too far off.

The overall formula is:

with the below values:

Variable Name	Training Data Mean	Coefficient Name	Coefficient Value (Rounded from R output)
Intercept	NA		0.0814
O-Swing	0.3087		-0.4480
Z-Contact	0.8702		-0.1120
Zone	0.4339		-0.4775
F-Strike	0.5986		-0.0565
O-Swing^2	NA		0.6144
F-Strike^2	NA		1.0372

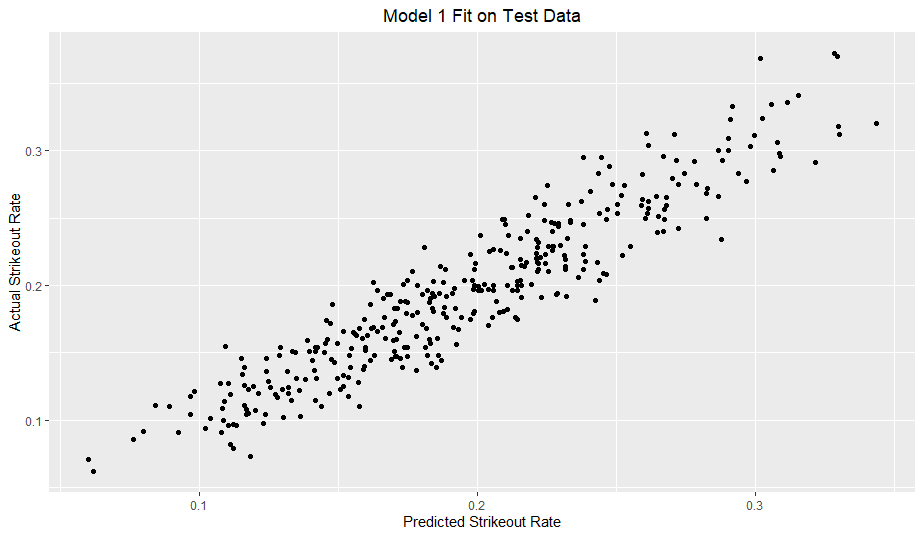
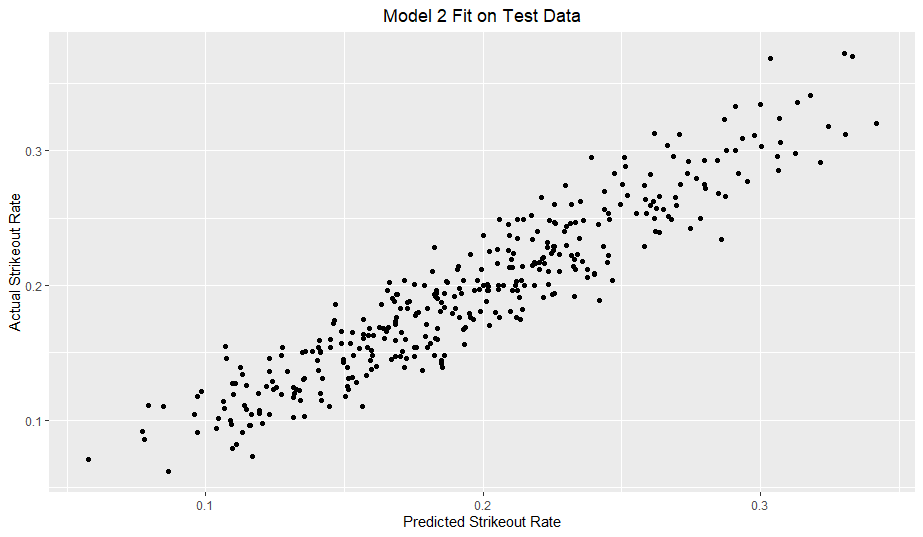
Here is the model fit on the test data:

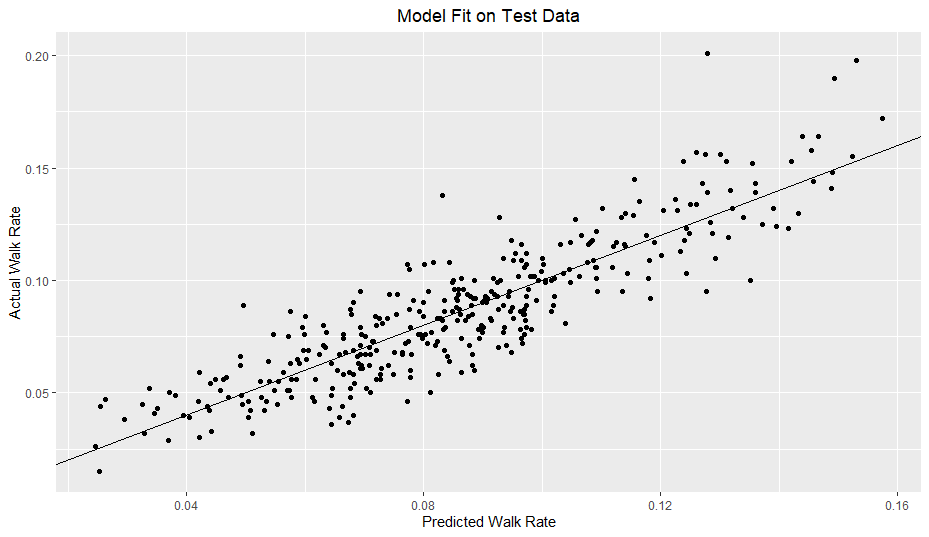
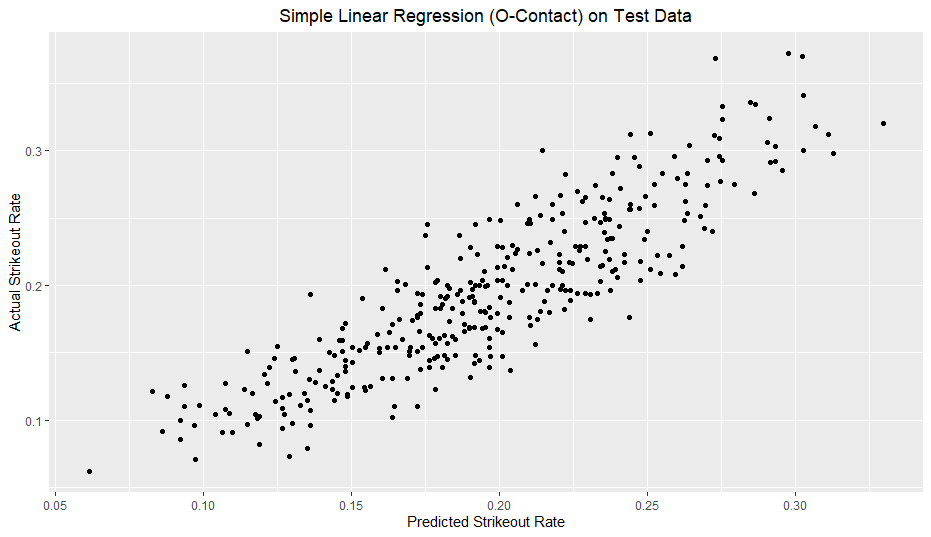
I added a reference line with a slope of 1 and y-intercept of 0. With a good model fit, the data should hug the line somewhat tightly. For reference, I included a model solely based on O-Swing and Model 2 from my previous article.

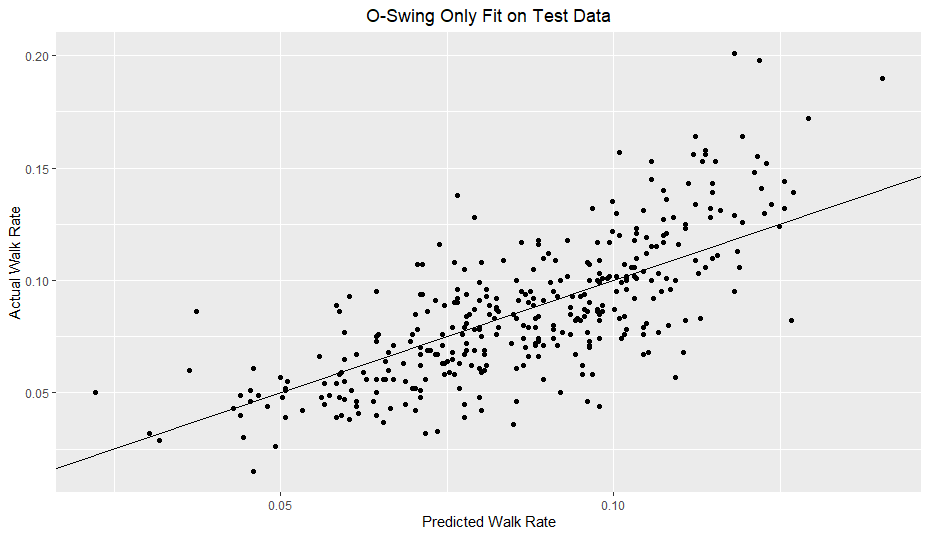
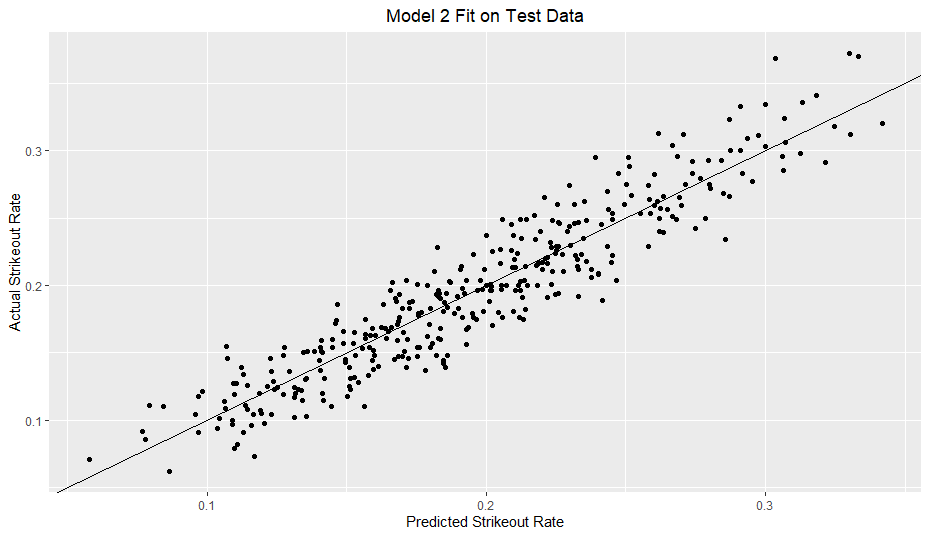
My model clearly outperforms the O-Swing only model. However, in comparison to my previous strikeout rate model, my walk rate model definitely does not hug the line nearly as well.

I thought that ridge regression could combat possible overfitting due to the polynomial terms but like last time, ridge regression did not help my model. Additionally, none of the regression tree models outperformed multiple regression. However, I will include a graph displaying variable importance for a random forest model I tested:

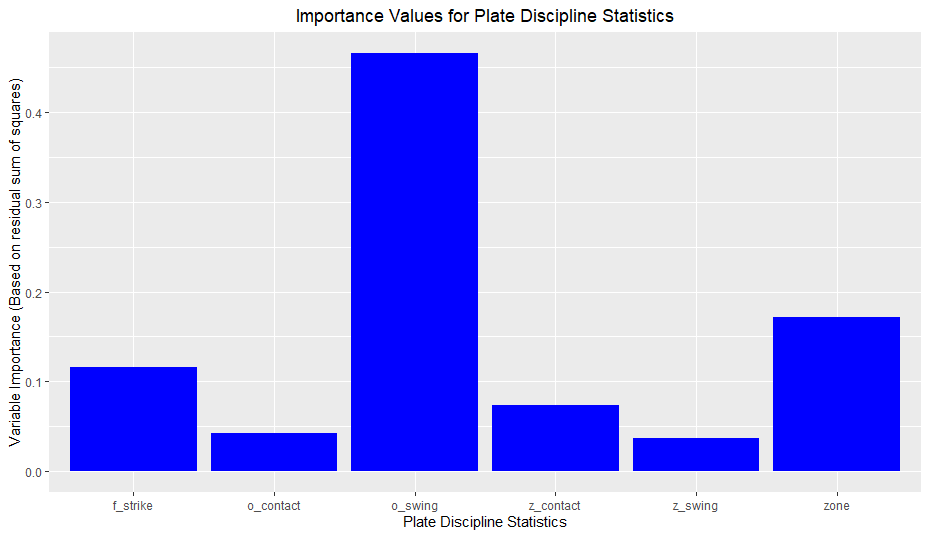
The graph aligns with my results from multiple regression; O-Swing is extremely important, whereas O-Contact and Z-Swing are minimally useful.

Conclusions

• High F-Strike and Zone values are linked to lower walk rates
• My model easily outperforms an O-Swing only model
• There was mixed/weak evidence for interaction terms

• O-Swing is the best and most important predictor of walk rate easily (among the plate discipline metrics I looked at)

My intuition on this was correct; O-Swing ended up being easily the most influential variable in my variable set. To reiterate, I reasoned that O-Swing was the only statistic that, in my opinion, had an obvious relationship with walk rate (swinging at balls is virtually always bad for taking walks).

• There is strong evidence for Z-Contact being linked to walk rates and much weaker evidence for Z-Swing and O-Contact

This is a complicated one; I don’t have a surefire answer why Z-Swing and O-Contact had less value relative to Z-Contact. However, I do have some ideas. In 2019, the league-wide values of O-Swing, Z-Swing, and Zone Percentage were 31.6%, 68.5%, and 41.8% respectively. Using basic dimensional analysis, I found that the percentage of total pitches that were both out of the zone AND swung at was roughly 18% whereas the percentage of total pitches that were in the zone AND swung at was about 29%. In other words, Z-Contact involves a greater number of pitches than O-Contact (29% vs 18%), perhaps leading it to influence walk rate to a greater degree.

In terms of the direction of the effect on walk rate, despite having a negative marginal correlation to walk rate, O-Contact actually had a positive coefficient (high values of O-Contact increase predicted value of walk rate) in a model with all of the main effects. I would expect more contact to generally lead to fewer walks, but in a case like fouling off a ball rather than missing it in a two strike count, making contact can help extend plate appearances and increase the probability of a walk. While the coefficient was positive, it was also quite small and had a low, but not minuscule p-value (about 0.02, based on robust coefficients). Whatever the coefficient sign though, I found only weak evidence for O-Contact being a useful variable.

As for Z-Swing, I expected it to have more of a negative effect, whereas in the main effect model mentioned above, it too had a positive coefficient, although with a large p-value of 0.29. In general, for these three statistics, their effect on walk rate is muddled because of the various influences they can have. A high Z-Swing, for example, would be positive (where positive refers to a higher walk probability) in a situation with two strikes in order to foul off balls and not take a called third strike. On the other hand, a high Z-Swing is a negative in most situations, as most swings in the zone end up resulting in contact and if the contact is fair, the chance of a walk becomes zero. Just like with O-Contact, Z-Swing doesn’t seem to play a big role in a walk rate model.

In summary, while you can argue which direction Z-Swing and O-Contact affect walk rate, my findings show that regardless of the direction neither statistic is particularly influential in modeling walk rate.

• There is significant evidence for F-Strike and O-Swing second degree polynomial terms

Like I discussed in the results, quadratic terms for F-Strike and O-Swing were supported with fairly strong statistical evidence. In terms of interpretation, it seems that for very large values of F-Strike and O-Swing, their effect on walk rate seems to level out, whereas for very low values, their effect is augmented. Despite the evidence, I caution accepting the quadratic terms as fact until further research is done.

• Simpler modeling (linear regression) performed better than more complex models (random forests, gradient tree boosting)

In my last post, I speculated that a more flexible model would improve performance. In this case, it did not. It appears that for walk rate and plate discipline, linear relationships (aided by quadratic terms) do seem to create better models than more flexible methods, which may be overfitting the data. However…

• Modeling walk rate (with plate discipline) is harder than modeling strikeout rate

As I pointed out in my results, the walk rate model did not evenly hug the reference line as well as my strikeout rate models. Because walk rate provides less information than strikeout rate given equal plate appearances, modeling walk rate, given equal plate appearances, will obviously be more difficult and have more noise. However, I don’t think it is purely noise. It seems that there is something “missing” in my model, which in turn causes heteroscedasticity. Like I mentioned earlier, my model generalizes worse on higher walk rates. It is possible, if not likely, that there are other variables (such as pitches per plate appearance) that would help my modeling but within the plate discipline metrics, I could not find them.

Limitations

• Not all strikes are equal and not all balls are equal

All of the limitations from last time apply here too, but I wanted to mention another limitation I glossed over. These plate discipline metrics treat every strike equally and every ball equally. A ball two inches outside is equal to a ball three feet outside here, which is not perfect. A potential solution is Statcast’s Attack Regions, which break up the zone into further subsections. However, dividing the strike zone further also reduces the sample size of pitches in each section, so there is a downside.

• Intentional Walks

As far as I know, these plate discipline metrics include intentional walk pitches from player-seasons before 2017. This inclusion *probably* does not affect the results meaningfully, as nearly half of the player seasons are after the 2017 rule change and the proportion of intentional walk pitches to overall pitches is quite small, but it could introduce some bias to the data.

Future Research

My next two pieces will conclude this series by looking at pitcher strikeout and walk rates. I suspect that pitchers will be a more difficult task, as I don’t think they have nearly as much control over their plate discipline statistics as hitters, but I could be mistaken. Thanks to Srikar for looking this over.

Strikeout and walk rates are perhaps the most popular and widely used peripheral statistics, particularly for pitchers. However, with pitch level data, these statistics now have “peripherals” of their own. I was curious if I could create an accurate yet interpretable model using FanGraphs’ plate discipline metrics that could offer insight on what drives the differences in strikeout and walk rates between players. For the first part in this study, I will focus on hitter strikeout rate, but I intend on also looking at walk rate and, later on, pitchers’ strikeout and walk rates.

Methodology

Note: I used BIS discipline statistics rather than PITCHf/x. I do not think this made a significant difference, but I think it is important to keep in mind.

FanGraphs gives us 9 plate discipline statistics to work with. However, several of them can be removed as they can be derived using the other statistics. In a regression setting, this phenomenon is called perfect multicollinearity, which is when an explanatory variable can be perfectly formulated by a linear function of other explanatory variables. Multicollinearity is a problem for inference because with a high degree of multicollinearity, it can be extremely difficult to tell which particular variable is responsible for a change in the response variable. In this context, Swing%, Contact%, and SwStr% are all examples of perfect multicollinearity. While they provide useful overviews for plate discipline, I would rather use their components for a regression to maximize the data’s information. An imperfect analogy is OPS. While OPS is a better overall offensive metric than either on-base or slugging percentage, I would rather have both on-base and slugging rather than OPS for more information on the hitter. Using some basic dimensional analysis, I found formulas for all three of these:

• Swing% = O-Swing% * (1 – Zone%) + Z-Swing% * Zone%
• Contact% = (O-Contact% * O-Swing% * (1 – Zone%) + Z-Contact% * Z-Swing% * Zone%) / Swing%
• SwStr% = (1 – O-Contact%) * O-Swing% * (1 – Zone%) + (1 – Z-Contact%) * Z-Swing% * Zone%

Note that while the formula for Contact% uses Swing%, you can simply plug in the formula for Swing% here to have a formula in terms of the other variables. After figuring out these formulas on paper, I also verified them with R.

Now we are down to 6 variables. At this point, I had a question; how quickly does each variable provide meaningful information about a hitter? To answer this, I did an informal check by looking at correlations between the first and second half values of these statistics using players from 2015 through 2019 who accrued at least 250 and 200 PA’s in the first half and second half respectively.

Statistic	First-Half to Second-Half Correlation
O-Swing%	0.827
Z-Swing%	0.833
O-Contact%	0.812
Z-Contact%	0.786
Zone%	0.664
F-Strike%	0.463
K Rate	0.794
BB Rate	0.713

I want to emphasize that this is a non-ideal way to figure out the information different statistics provide. For example, the correlation method doesn’t account for any potential plate discipline erosion that occurs over the season. For a better approach, I would check this out. However, for our purposes, I think it gives us a rough idea of the information the statistics provide. For the first four variables, it appears that, at the very least, they provide equal if not better information than either strikeout or walk rate given equal plate appearances. On the other hand, zone and first-pitch-strike rate seem to provide less information given equal plate appearances than the other statistics. I will still experiment with them in the regression, but these correlations will definitely impact and qualify my interpretations.

Next, I created the data set for the regression, using all player seasons from 2012 through 2019 with at least 400 PAs. I chose 2012 as my starting point for several reasons. Firstly, it was the first year that strikeout rate began to increase league-wide. I was worried that if I went too far back, the strikeout environment would be too different from recent years and perhaps couldn’t be modeled in the same way as current day. However, I still wanted to have as much data to build my model as possible, so I felt that 2012 was a good compromise as a cutoff year. I chose 400 PA’s somewhat arbitrarily, but I thought it was a good cutoff point as the reliability for both strikeout and walk rate are above 70% and 400 is still a low enough limit to create a fairly large dataset. There were 1657 player seasons that met the above criteria.

Before splitting my dataset, I looked at the individual correlations between the variables and strikeout rate. The two highest were Z-Contact with -0.851 and O-Contact with -0.868. Hopefully, my model will be able to significantly outperform both of these two variables on their own.

Next, I randomly divided the observations up, giving 1000 to my training set, 300 to my cross validation (CV) set, and 357 to my test set.

In addition to my main terms, I also tested 4 interaction terms and polynomial terms up to the third degree for every variable. When formulating possible interaction terms, I thought that the swing, contact, and zone variables could have a potential synergy effect. For example, if a hitter swung a lot out of the zone AND also didn’t make much contact on swings out of the zone AND received a lot of pitches outside of the strike zone, it makes sense that this hitter may have a higher strikeout rate than one would assume from simply looking at O-Swing%, O-Contact%, and Zone% independently. This brings me to an important change I made: I used O-Miss% = 1 – O-Contact% instead of O-Contact% and Non-Zone = 1 – Zone% instead of Zone% in order to consider some of these interaction effect. Overall, I tested O-Swing * O-Miss, O-Swing * O-Miss * Non-Zone, Z-Swing * Z-Contact, and Z-Swing * Z-Contact * Zone. I also mean-centered my main terms to help interpretability and lower multicollinearity introduced by the polynomial and interaction terms.

Generally, whenever you include interaction terms in a regression, you also keep the individual terms that compose the interactions, even if they aren’t particularly helpful for the regression. However, because Non-Zone% and Zone% are redundant, I just used Non-Zone% in my regressions instead of including both.

Lastly, I wanted to discuss the several regression methods I modeled with. I used standard multiple regression, the lasso, and ridge regression. To implement the lasso and ridge regression, I used the glmnet R package. To select a value of lambda, I used cv.glmnet() and supplied a range of lambda values to perform cross validation on. Big shout out to the authors of ISLR. Their sample code in the textbook was an excellent reference for me and ISLR is also an excellent way to learn about statistical learning for those interested.

If you have any more questions on my methodology, you can either comment, tweet at me, or check out my Github. However, because this is an ongoing series, I probably will not update my Github with the code for this project until the whole series is done.

Results

Model 1

I will share the results of two models. The first model is the basic multiple regression with only main effects, minus O-Swing%, which I omitted due to its small coefficient and limited improvement to the cross validation mean squared error (CV MSE).

While this model did not have the lowest CV MSE, it was in the ballpark of the best MSE and also was the simplest and most interpretable model. Below, I compared this model to two simple linear regression models based on O-Contact and Z-Contact, as they were the two explanatory variables that correlated the most with strikeout rate.

The overall formula is:

with the below values:

Variable Name	Training Data Mean	Coefficient Name	Coefficient Value (Rounded from above output)
Intercept	NA		0.196
Z-Swing	0.6745		-0.229
O-Contact	0.6603		0.346
Z-Contact	0.8702		-0.621
Non-Zone	0.5661		0.148
F-Strike	0.5986		0.133

As you can see, the main-effects only multiple regression far outperformed models solely based on O-Contact and Z-Contact, with test MSE’s roughly double for the simple linear regression models.

The residual plot seems to be quite random and scattered with little evidence of heteroscedasticity, but the model fit on the test data shows some very slight heteroscedasticity for high values of strikeout rate.

Next, here is the model with the best (roughly) CV error. While a few other models had slightly lower CV errors, I chose this one as it was the simplest in that group and had low p-values for all of its terms. However, I do want to mention that even though it has the lowest CV error (again, roughly), it is not significantly lower than the above model and secondly, the interaction terms make it harder to interpret.

Model 2:

The overall formula for Model 2 is:

Variable Name	Coefficient Name	Coefficient Value
Intercept		0.196
O-Swing		0.054
Z-Swing		-0.246
O-Miss		0.357
Z-Contact		-0.628
Non-Zone		0.108
F-Strike		0.094
O-Swing * O-Miss		0.294
O-Swing * O-Miss * Non-Zone		-8.582

The training data mean for O-Swing is 0.3087 and the rest of the means are in the previous table.

This residual plot also seems quite randomized, and the slight heteroscedasticity in the fit seems even more minor here.

Additionally, I chose not to include any of my lasso or ridge regression models. Neither outperformed standard multiple regression in terms of CV MSE.

As you can see, the tuning parameter lambda seemed to produce the smallest MSE for the values closest to 0 and when lambda equals 0, both lasso and ridge regression just become standard multiple regression. This graph was generated with cv.glmnet()’s default lambda values which can be very odd, but when I tested with my own lambda list, 0 was often chosen as the ideal lambda. In other words, 0 (or close to 0) seems like the ideal value of lambda, which means both lasso and ridge regression don’t provide much over standard multiple regression. Because I had a relatively high number of observations and relatively few predictor variables, all of which seemed to have linear relationships with the response, it makes sense that there was little overfitting for the lasso and ridge regression to correct.

Lastly, for both models, all terms, including interactions, had VIF values all well under 5, which is great from a multicollinearity perspective.

Analyzing Interaction Terms

Before getting into my overall interpretations and conclusions, I wanted to analyze the interaction terms in my second model.

Two Term Interactions

The above graph is perhaps the most significant result of my entire project. I created this graph using the sjPlot package. In this graph, the green, blue, and red lines correspond to the value of O-Miss one SD above the average, the mean value of O-Miss, and the value of O-Miss one SD below the average respectively. Notice that the mean of O-Miss is zero, as I mean-centered all the main effects. As you can see, for a higher value of O-Miss, the corresponding increase in predicted Strikeout rate accompanying an increase in O-Swing is larger, shown by the slope in each line. Even though the starting point of the green line is highest, it also has the steepest slope of any lines. On the other hand, when O-Miss is small, the slope is smaller, meaning that a larger O-Swing boosts the predicted strikeout rate less than a simple linear model would expect. Essentially, Model 2 suggests that there is a synergistic relationship between O-Swing and O-Miss, as I suspected. However, the p-value, while under the general 0.05 threshold, is not minuscule, so I would not say that this relationship exists with certainty.

On the other hand, the Z-Swing * Z-Contact interaction term showed little evidence of existing in the training set, which is why I omitted it from Model 2.

Three Term Interactions

While the training data gave evidence for the O-Swing * O-Miss * Non-Zone interaction term, its third dimension makes interpretation much more difficult.

Looking at this data, I really cannot see a unifying interpretation. The slopes seem to equalize as you go from the left to right graph, possibly indicating that the O-Miss * O-Swing interaction term is stronger for lower values of Non-Zone (i.e. more pitches in the strike zone), but I’m not really sure why that would be. I also found the red line in the far left facet interesting. Essentially, for hitters who get a lot of strikes and do not miss on pitches out of the zone too much, O-Swing really does not affect Strikeout Rate for this model very much. This does make some sense, as these hitters deal with fewer pitches out of the strike zone and also make contact on those non-zone pitches more often so the effect of their O-Swing is minimized. Feel free to share any observations you can see from the above graph. The p-value for this interaction term is also not exceedingly small and because of its lack of intuitive reasoning, I would treat this term with even more skepticism.

Similarly to the two-term interaction, the Z-Swing * Z-Contact * Zone interaction term showed was not statistically significant in the regression and did not meaningfully lower the CV MSE.

Interpretations and Conclusions

There are three fairly basic and obvious interpretations I’ll mention briefly:

• Swinging and missing in and out of strike zone generally increases your strikeout rate
• Swinging more in the zone generally lowers your strikeout rate
• Both of my models far outperformed simple linear regression models based on O-Contact and Z-Contact, the two main effects most directly linked to Strikeout Rate, on the test set

I find these two points more interesting:

• More pitches in the zone generally corresponds to a lower strikeout rate
• More first pitch strikes correspond to a higher strikeout rate

As I noted in the methodology section, Zone/Non-Zone and especially F-Strike had lower first-half/second-half correlations than the other variables. Zone still had a 0.664 correlation, which makes me suspect that there is some predictability in a hitters Zone%. Specifically, I wonder if a higher Zone% is not causing lower strikeout rates but rather is a reflection of pitcher’s perception of the hitter as a dangerous or strikeout-prone hitter. For example, by 2015, most pitchers should know that Ben Revere is not a particularly strikeout prone or intimidating hitter. Thus, he received more pitches in the strike zone than most hitters. In other words, Zone isn’t causing a change in strikeout rate; rather it could partially reflect the general perception of a hitter’s strikeout ability from prior data, which ends up making Zone a useful predictor in what the strikeout rate “should” have been. Zone, rather than being an independent variable in the regression, could be a crude estimation of past strikeout rate, although there could be hitters with low strikeout rates who chase a lot and are thus given fewer pitches in the zone. However, this is conjecture and the project’s limited scope does not really give us insight on what drives Zone% for hitters.

With F-Strike, I think some of my conjecture on Zone could be applied here but with only a correlation of 0.463, it doesn’t seem as stable or interesting to me. I will say, though, I did not expect F-Strike to play much of a role at all. I underestimated the effect a first pitch strike can have on the overall trajectory of a plate appearance.

• O-Swing does not, as a standalone variable, contribute very much to a linear model.

While O-Swing did play a role in interaction terms, it individually did not have a large effect in my models. It seems somewhat counterintuitive, as you would expect that swinging at balls would correspond with a strong increase in strikeout rate, whereas I found that the increase was very small. However, you can be a free swinger and maintain a low strikeout rate if you make enough contact, like Jose Iglesias for example. Conversely, Z-Swing had a much stronger effect on strikeout rate, which muddles things up somewhat.

• There is evidence for the interaction terms O-Swing * O-Miss and O-Swing * O-Miss * Non-Zone being meaningful

Both of the above terms were statistically significant using the coefficient p-values (under 0.05), but not overwhelmingly so. I think these findings warrant further study, particularly for the O-Swing * O-Miss term, as it also has a reasonable interpretation.

Conversely, Z-Swing * Z-Contact and Z-Swing * Z-Contact * Zone had little statistical evidence for existing in the actual model.

• Polynomial terms had no statistically significant evidence for any variables

Both in terms of p-values and CV MSE, I could not find any evidence for polynomial terms up to the third degree for any explanatory variable.

Limitations

While I think this project had some interesting findings, there are several limitations I wanted to bring attention to.

• Plate Discipline does not consider the ball-strike count

FanGraphs’ plate discipline metrics treat every pitch equally; however, in a real plate appearance, the count matters tremendously. While I haven’t personally verified it, it is very likely that plate discipline changes within certain counts, like Joey Votto choking up with two strikes. Treating a swing and a miss in an 0-0 count versus a two strike count equally is not ideal, but it is the reality when working with these metrics.

• Bias with Multiple Regression

As the lasso/ridge regression tuning parameter graph showed, overfitting did not seem to be a major issue. However, I do think underfitting could be a problem with a simple, inflexible model like multiple regression. While fitting various models, I noticed that adding interaction terms, even ones with large standard errors and high p-values, nearly always reduced the CV error, even if only marginally. I do think that using a more flexible method, such as splines, would perform better from an MSE/performance perspective, but I am happy with the interpretive value multiple regression gave for this project.

• Descriptive rather than Predictive

An important asterisk on my models is that they are not meant to be predictive. Firstly, several of the explanatory variables, namely Zone and F-Strike, are not extremely stable as shown in my rudimentary correlations earlier. Even though they added value to my models, they are not stable enough to extrapolate an input from the models as a baseline strikeout rate going forward. Secondly, these models do not take into account age, changes that come about due to change, etc. Lastly, related to my previous point, these models were built to balance interpretation and accuracy, not maximize accuracy, so I would not recommend using it in a predictive way, even if you ignore the above reasons.

• Assumption of Underlying Model Consistency

Because I used data from 2012 onwards, I’m implicitly assuming that the underlying hitter strikeout model is consistent despite various league hitting trends. If this assumption was not true, the validity of my results would be questionable. However, even with the large but not drastic leaguewide shifts, I see no reason why the underlying model would change significantly, especially in regards to inference. Swinging and missing more should be linked to more strikeouts, regardless of the environment. While different environments could make swinging and missing less impactful, the overall inferences from my models should not drastically swing from year to year.

What’s Next?

As I said earlier, I intend on using this same methodology for hitter walk rate and later on, looking at discipline metrics from a pitcher standpoint. I’m curious to see how the O-Swing * O-Miss interaction term acts in these situations. Additionally, this project piqued my interest in how pitchers approach different hitters and how meaningful differences in pitching strategies are. I’m glad I undertook this project, as it gave me a chance to implement several different kinds of regression and deal with all that entails (selecting tuning parameters, checking residual plots, etc.). While linear regression is a useful tool, I also hope to apply some more technical machine learning algorithms (if you can even call linear regression machine learning) in the future.

Thanks for reading! If you want updates on my future work, you can follow me on Twitter here. A big thanks to Srikar and John for looking this over.

With the advent of Statcast, statistics like exit velocity, spin rate, and launch angle have become easily accessible to baseball fans. Catcher pop time data, too, has become available from Statcast. However, unlike some of the other Statcast metrics, catcher pop time data has existed for much longer, with scouts measuring pop times in the minor leagues years before Statcast entered the mix.

This sounds all well and dandy right? Well, it would be, if the Statcast numbers were consistent with scouting pop time tool grades. BP, for example, calls a pop time from 1.7-1.8 a 70 pop time, which sounds reasonable enough without any context. However, considering the highest average Statcast pop time to second base from 2015 to 2019 was JT Realmuto’s 1.88 (minimum 10 throws to second), something seems amiss here. I decided to take a deeper look into Statcast’s pop time data to get a better idea of what’s going on.

Methodology

First, I downloaded all of the catcher pop times from Baseball Savant, minimum one throw to second base, from 2015 through 2019. Each player-season combination is its own data point (i.e. JT Realmuto’s 2018 and 2019 pop times are separate data points). Next, I combined these CSV files into one big data set.

From this data set, I created two new data sets. In the first data set, I set a 10 throws to second base minimum. This is the data set I am using in this article. In the second data set, I tried to weight every throw equally. The first set treats every player that meets the minimum as its own equal data point; that is, no matter if a player had 10 throws or 50, they are equally weighted. However, in the second data set, I first dropped the throw minimum and then replicated each player’s average pop time by the amount of throws they had to create the data set. This is easier to understand with an example. Let’s say the data set had Catcher A with 2 throws at an average of 1.84 seconds, Catcher B with 3 throws at an average of 1.99 seconds, and Catcher C with only 1 throw at 2.04. The data set, using the second methodology, would be (1.84, 1.84, 1.99, 1.99, 1.99, 2.04). Unfortunately, because Statcast only offers average pop times and not each individual pop time, I cannot truly account for each and every throw but I think this is a pretty good alternative.

The main reason I used these two different approaches was because of the variety of ways one could evaluate tool grades for players. On the one hand, a 50 grade tool could mean the average of player averages. On the other hand, an average tool could be the actual numerical average of that tool, such as a 50 grade exit velocity tool being equivalent to the average exit velocity of every single batted ball. I will discuss the results of the second approach more in depth in a follow up article.

Based on the data, I created new pop time tool grades. I did this simply by finding the standard deviation of the sample and adding/subtracting SDs to the mean to find all the grades. As a reminder, a 10 point difference in scouting grades represents one standard deviation shift in the tool. I also created another set of tool grades based on the Empirical Rule, as the distribution seemed approximately normal. I tested the normality of the data sets using the Anderson-Darling test along with Q-Q plots. The first data set passed the AD test (p-value greater than 0.05) and had a very linear Q-Q plot, so it is safe to say the data set is approximately normal.

For more insight on my methodology, you can check out my Github here. My code for this project is in the Project 3 folder.

Results

These graphs simply plotted the average pop times of catcher seasons from 2015 to 2019. As I established earlier, the distribution is approximately normal which the blue normal curve demonstrates by fitting the data quite nicely.

Next, I graphed the blue normal curve above with a red normal curve based on Baseball America’s catcher arm strength grades from the 2018 Prospect Handbook. Their 50 grade pop time was 1.95-2.04, so I simply averaged the two to find the mean and used 0.10 as the standard deviation to create the red normal curve.

There are two main takeaways from this graph. Firstly, the Statcast curve has a slightly higher mean than the BA curve. Secondly and more notably, the Statcast data has far smaller spread than the BA grades, in both directions. Like I said earlier, the highest average pop time grade from 2015 to 2019 was 1.88 (Realmuto’s 2019), which would only be a 60 grade pop time according to both Baseball America and Baseball Prospectus. Clearly, there is a strong disconnect between Statcast pop times and traditional scouting grades.

Using data set 1, I created two new pop time grade scales. The Empirical Rule scale is based on, you guessed it, the Empirical rule for normal distributions. The Data Scale is simply based on the actual standard deviation of the data rather than assuming the percentiles and standard deviations match up a certain way like the Empirical rule does.

The BA Grades were ranges rather than concrete values, so I just averaged the ranges to find the grades.

Tool Grade	BA Pop Times	Empirical Rule Pop Times	Data Pop Times
80	< 1.74	< 1.89	< 1.85
70	1.795	1.93	1.90
60	1.895	1.99	1.96
50	1.995	2.01	2.02
40	2.095	2.04	2.07
30	2.195	2.10	2.13
20	> 2.25	> 2.16	> 2.18

Conclusions

Obviously, something strange is happening here. While I don’t know why this is the case, I’ve thought of a couple potential explanations.

1. Measurement Error. To the best of my knowledge, scouts typically measure pop times using a stopwatch. Perhaps the human error with stopwatches is a contributor, or the Statcast measurements are off.
2. Different Measurement Methods. The most common definition of pop time is “time elapsed from when the catcher catches the ball and the fielder catches the throw.” However, Statcast pop times measure “the time elapsed from the moment the pitch hits the catcher’s mitt to the moment the intended fielder is projected to receive his throw at the center of the base”. This seems to imply that catching the ball in front of the base would underestimate pop times relative to the Statcast measures. While this explanation makes sense, it doesn’t explain why the mean Statcast pop times aren’t significantly higher than the scouting pop times.
3. Max Pop Time versus Average. Some scouts could grade pop times based on maximum pop times rather than averages, which is what data set 1 is comprised of. Once again, this doesn’t explain why the averages are relatively close.
4. Catching Arm Talent is Down. Perhaps the current major league catcher arm talent is lower than it typically is.
5. Total throws versus averages. This is essentially what I talked about in my methodology, and is why I wanted to look at two separate data sets. Spoilers on the results of data set 2; the distribution was essentially the same to data set 1, so this probably isn’t the issue.

I am really curious if anyone in the scouting industry or from Statcast has any explanations for this discrepancy. I will try to reach out and see if I can get an answer.

While labeling pop times doesn’t actually change how hard catchers are throwing, I think this issue is very important from a data consistency standpoint. When you evaluate minor league players, you want to be sure that you properly contextualize their tools from a current major league standpoint. Assuming the data measurements on both the scout and Statcast sides are accurate, then it’s possible that the scouting industry should reevaluate their pop time tool scale.

Within the next few days, I will also put up my results for data set 2, although they aren’t much different. If you are interested in reading about my future projects, you can follow me on Twitter here. Thanks to John Matthew and Srikar for looking this over and thanks for reading!

Introduction

As an LSU alumni, Aaron Nola has long been said to be at his best in blistering hot weather. Many writers and Phillies fans believe that warm, muggy weather meaningfully improves his pitching performance. I wanted to see if I could find any evidence for this belief.

Here is a graph looking at Nola’s career FIP by month:

This should be a decreasing bar graph if the belief said earlier is true, as temperature rises through the baseball season. However, temperature can fluctuate significantly within a month so for this study, I will be doing a deeper dive into the game-by-game weather data.

Methodology

As in my previous inquiry, I used R and RStudio. I focused in on two weather factors; temperature and relative humidity. I am no meteorologist, but my understanding of relative humidity is that it is a measure of the total amount of humidity possible at a certain temperature. Because it isn’t reliant on temperature like absolute humidity, I can use it as an independent variable from temperature. If Nola really does pitch better during hot and humid weather, one would expect his best games occur when both temperature and relative humidity are very high.

As I said earlier, I decided to look at weather data on a game-by-game basis rather than monthly stretches. I used to two main sources for finding my weather data: Retrosheet and the Riem package. I do not have any webscraping skills (yet), so I used the Retrosheet gamelogs’ DayNight variable to estimate the times in a similar method to this study. If it was a day game, I approximated the start time as 1 PM local time and for a night game, 7 PM. My weather data was based on these approximate start times, using the temperatures and relative humidities measured closest to the start times. The Riem package has a function, riem_measures(), that returns all weather data measured at a given airport over a stretch of dates. I found the closest airport for each ballpark Nola pitched in and used the airport code to acquire the data.

To measure the quality of each start, I used Tom Tango’s Game Score Version 2.0. via FanGraphs’ gamelogs. I also looked at Nola’s average curveball spin rate from Baseball Savant in each start to see if the weather played a role there.

Important Note: I only looked at data from the 2015 through 2018 seasons, as Retrosheet has not released its 2019 Gamelogs yet.

For more info on my methodology, check out my code here. My code is full of my thought process, so any further questions you have will probably be answered there. If not, feel free to comment and I will answer as soon as possible.

IMPORTANT QUALIFIER ON WEATHER DATA

The riem package gets its data from the Iowa Environmental Mesonet. However, after cross-referencing some of my data points with Weather Underground, I found significant differences in temperature. I made a function to add the weather data to my overall data, so I first checked if an error in my function was leading to the data differences. My function would find the temperature and humidity of at the time closest to my estimated game start time. I checked several of my data points to make sure my function was getting the data from the closest time. These checks were all fine. This means that the Iowa Mesonet data simply varies from Weather Underground data. I don’t know if this is due to different measurement locations, altitude, etc., but I think this variation is an important qualification to my results, as I don’t know how trustworthy this data is. Also, for clarity, I did not use Weather Underground data because, as I said earlier, I have not learned how to webscrape and the rwunderground package no longer works.

Results

Before getting into my actual graphs, here is a sample graph:

This graph is just meant to give a general idea of what the data “should” look like if Nola actually does pitch better in certain weather conditions. Obviously, temperature and relative humidity are independent so they shouldn’t be assumed to have a linear relationship, and the units of the axes are way off, but that isn’t the goal of this graph. Each point has a color corresponding to an individual game score. The lighter the shade of blue, the higher the game score. So, if humidity and temperature do help Nola, we should expect values to be very light in the upper right corner and very dark in the lower left corner (i.e. high temp + high humidity implies higher game scores). Now, for the actual graphs.

Looking at the three variable graph, I do not see much of a trend. The light colored points do not seem to cluster anywhere, except in the bottom right corner. This would imply Nola performs best in non-humid but hot climates, but this observation is not strong enough for me to seriously believe this.

Looking at the individual effects of temperature and humidity on game score, I also do not see much here. For both graphs, I included a trend line using LOWESS smoothing, which shows the relationship between two variables without assuming a variable relationship (linear, logarithmic, etc.). For temperature, I see an increase in the trend line in the data at extreme temperatures (above 90 degrees), but the vast majority of the data has no trend. I don’t see anything in the humidity graph that would support the “Nola weather hypothesis”.

Here are the graphs for curveball spin:

There is even less of a visible relationship than the previous graphs. It seems that neither temperature nor humidity have a significant effect on curveball spin.

Both the trend lines and the actual data points indicate neither temperature nor humidity have an effect on curveball spin rate.

Conclusions

The data and the graphs above do not support the belief that Aaron Nola pitches better in hot and humid weather. Like I mentioned earlier, the weather data from the Iowa Environmental Mesonet does not match up with the data from wunderground, so my results could be impacted by unreliable weather data. This is an extremely important qualifier to this project as if the data is unreliable, it cannot generate any valid conclusions. However, assuming that this data is credible (and the Iowa Environmental Mesonet does appear to be a reputable data source), I found no strong evidence of weather affecting game score and curveball spin rate. There was some evidence of better game scores at temperatures above 90 degrees, but the evidence consists of less than 10 starts, so I would not draw strong conclusions from it.

Nola only pitched roughly 100 starts from 2015 through 2018, so the amount of data I worked with is limited. Perhaps with more starts and more consistent weather data, Nola would demonstrate a performance improvement in hot and humid environments. However, I suspect that while Nola might feel more comfortable pitching on warmer days, this comfort does not meaningfully boost his performance relative to other variables. Opponent quality and fatigue down the stretch, to name a few other variables, likely play a larger role in his performance variations than the weather that day.

The weather’s effect on individual player performance is complicated. While conclusions on weather conditions affecting baseball on a broader scale can be found and strongly supported (higher temperature leads to higher home run rate, for example), identifying that a player performs better under certain conditions and figuring out if there is a meaningful reason why is a more daunting task. Does the increased humidity help him grip his pitches better and improve spin rate? Or does it slow down his pitches and make them easier to hit? How much of this improved performance is noise due to small sample or related to other variables? In other words, it is difficult to draw any meaningful conclusions about weather affecting individual players, due to numerous interpretations and relatively small sample.

Future Projects

For the reasons above, I don’t plan on revisiting weather data any time soon. If I do, I would want to do some reading on the physics of baseball so I would actually know what is physically happening with the baseball. As for my next article, I plan on analyzing Aaron Nola again, but that is all I will say for now. School has been somewhat taxing and prevented me from finishing this project sooner. With winter break coming up and an easier schedule next semester, I hope to be more active on this blog. Follow me on Twitter if you want to see any of my future work. Thanks to my friends John Matthew and Srikar for looking this over.